Représentations graphiques

Python est muni de modules avancés permettant de faire de n'analyse numérique numpy et de tracer des représentations graphiques diverses matplotlib . La syntaxe n'est pas très éloignée de matlab ou scilab.

IImporter les modules

On peut taper directement les deux lignes d'import :
import numpy
import matplotlib.pyplot
Cela signifie qu'il faudra taper des commandes assez longues du type matplotlib.pyplot.plot(x,y) . Pour éviter ce problème, on va utiliser des alias...
On peut donner des alias aux modules utilisés :
import numpy as np
import matplotlib.pyplot as plt
Créer un fichier courbes.py et importer les deux modules avec les alias.
Si vous souhaitez éviter de faire précéder chaque instruction par np ou plt , il est toujours possible d'utiliser la syntaxe :
from numpy import *
from matplotlib.pyplot import *
Des erreurs peuvent se produire si des fonctions d'autres modules possèdent le même nom...

IITracé de points

Pour tracer une ligne brisée à partir d'une liste de points, il faut en fait deux listes : la liste des abscisses x et la liste des ordonnées y . Il faut utiliser la commande plot :
plt.plot(x,y)
Si la courbe ne s'affiche pas directement dans la console, ajouter la ligne :
plt.show()
Tracer la ligne brisée passant par les points \(A (1,4), B (4,4), C (1,1), D (4,1)\).
Cliquer pour voir la solution
Replier
Il faut séparer les abscisses des ordonnées :
x = [1, 4, 1, 4]
y = [4, 4, 1, 1]
plt.plot(x, y)
Par défaut les points sont reliés par une ligne bleue d'épaisseur 1 pixel et les points ne sont pas marqués. Ces paramètres sont modifiable (voir partie options de tracé).

IIITracé d'une courbe

La courbe ne sera pas réellement tracée, mais plutôt une ligne brisée avec un pas suffisamment fin pour s'en approcher visuellement. Il faudra utiliser la fonction linspace du module numpy pour créer une liste compatible avec les fonctions mathématiques :
x=np.linspace(départ, arrivée, nombre_de_points)
y=ma_fonction(x)
plt.plot(x,y)
Pour tracer la fonction \(f (x) = sin(x)\) sur \([0;2 \pi]\), on écrira :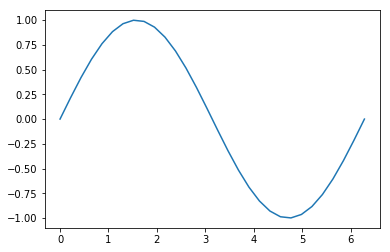
x=np.linspace(0, 2*np.pi, 40)
y=np.sin(x)
plt.plot(x,y)
Reproduire l'exemple précédent.
Le module numpy contient les fonctions mathématiques usuelles et les constantes, accessibles ici en préfixant par 'np' le nom de la fonction : np.nom_de_la_fonction
Voici quelques fonctions et constantes usuelles. Cliquer ici pour une liste complète.
np.sin() sinus
np.cos() cosinus
np.sqrt() racine carrée
np.abs() valeur absolue
np.log() logarithme népérien
np.exp() exponentielle
Pour tracer plusieurs courbes sur le même graphique, c'est assez simple :
x=np.linspace(départ, arrivée, nombre_de_points)
y1=f1(x)
y2=f2(x)
plt.plot(x,y1) plt.plot(x,y2)

Tracer sur le même graphique les fonctions usuelles définie sur \([0;2]\) : identité, carré, inverse, racine, cube.

Nous reviendrons sur cette figure

IVOptions de tracé

Il est possible de choisir des options pour mettre en forme ses courbes, ses nuages de points et une légende.

1Points et lignes

Pour changer la forme et la taille des points et des lignes, ajouter np.plot(x,y,'o') . Voici quelques options :
'o' nuage de points ronds
'o-' courbe + points ronds
'--' courbe en pointillés (sans points)
's:' points carrés (s) et pointillés fins (:)
x-. points croix (x) et pointillés moyens (-.)
Cliquer ici pour une liste complète des options.

2Couleurs

Pour changer la couleur, ajouter np.plot(x,y,'r') . Voici quelques options :
'r' rouge
'g' vert (green)
'b' bleu
'm' magenta
c cyan
w blanc (white)
k noir
Ces couleurs sont composables avec les options de formes des points et des courbes.
La commande plt.plot(x,y,'rx-') trace une courbe pleine avec des points rouges en forme de croix.
Revenir sur la figure des fonctions usuelles, et donner une couleur différente pour chacune. Mettre la droite d'équation \(y=x\) en pointillés.

Il est possible de choisir n'importe quelle couleur par son code hexadécimal plt.plot(x,y,color='#ff6699') .

Choisir par exemple sa couleur sur ce site .

3Largeur de ligne

Pour changer la largeur de la ligne, indiquer l'épaisseur via l'argument linewidth en indiquant un nombre : plt.plot(x,y,linewidth=2) .

4Légende

Pour ajouter une légende, il faut d'abord indiquer un label pour chaque courbe tracée comme ceci :
plt.plot(x,y,label='description').
Puis après le tracé des courbes, afficher la légende comme ceci :
plt.legend().
x = np.linspace(0, 5 , 30)
y1 = 2*x+1
y2=x**2-1
plt.plot(x, y1,'r', label='affine')
plt.plot(x, y2,'b', label='second degré')
plt.legend()
Revenir sur la figure des fonctions usuelles et ajouter une légende pour chaque fonction indiquant sont nom.

5Réglage des axes et de la fenêtre

Pour régler la fenêtre d'affichage, on peu préciser un domaine en ajoutant :
plt.xlim(xmin, xmax) plt.ylim(ymin, ymax)
Revenir sur la figure des fonctions usuelles forcer l'affichage pour \(x\) sur [0;2] et \(y\) sur \([0;2]\)
Pour que le repère soit orthonormé, il faut écrire plt.axis("equal")
Revenir sur la figure des fonctions usuelles et afficher une figure non déformée. Ajuster les valeurs xmin , xmax , ymin et ymax .
Tracer la figure suivante :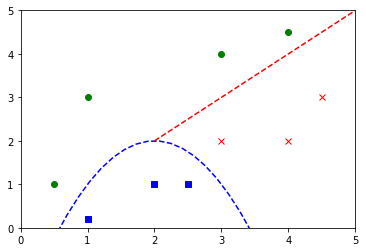
Le module matplotlib permet d'aller beaucoup plus loin dans les représentations graphiques (3D, histogrammes, coordonnées polaires, images, projections, etc.). Cliquer ici pour voir des exemples.

VTracer un rectangle plein

Ca fait un peu sorti de nulle part, mais nous en auront besoin dans le prochain TD...
Pour tracer un rectangle plein, il faut en premier récupérer la référence des axes (get current axis) :
axes = plt.gca()
Puis paramétrer le rectangle en donnant le point de départ (en bas à gauche), la largeur et la hauteur :
rect=plt.Rectangle((x0, y0), largeur, hauteur, color = 'red')
Enfin le tracer (c'est là qu'on a besoin des axes) :
axes.add_patch(rect)
Revenir sur la figure des fonctions usuelles et séparer les zones \(x \lt 1\) et \(x \gt 1\) à l'aide deux rectangles colorés par dessus lesquels seront tracées les autres courbes.